Introduction

Finite state machines are a model of computation that consist in a set of states, a set of input symbols, a function that maps every tuple (input, state) to new state and the actions performed at each state. A complete exposition of the concept is beyond the scope of this documentation. Here we will show how coroutines are a straightforward implementation of this model.

Sequence recognizer

Consider a state machine that implements this behavior:

In practice it is a sequence recognizer.

The formal description of this state machine is the following:

The initial state is A. This FSM can be represented by the following Meley model:

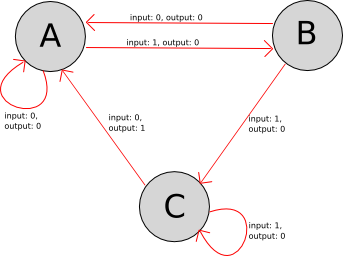
For example, given the input:

0110100010010001101001000111110010011001

The output will be:

0001000000000000010000000000001000000100

This state machine can be implemented in C++ directly from it definition, using a switch statement inside a stateful function object:

struct fsm {
  void operator() (char input_) {
    bool input = input_ != '0';
    switch(m_state) {
    case A:
      std::cout <<"A";
      m_state = input? B : C;
      break;
    case B:
      std::cout <<"B";
      m_state = input? C : D;
      break;
    case C:
      std::cout <<"C";
      m_state = input? B : A;
      break;
    case D:
      std::cout <<"D";
      m_state = input? A : C;
      break;
    };
  }

  fsm() :
    m_state(A) {}

  enum state { A, B, C, D};
  state m_state;
};

Each case block directly implements its corresponding state. While the transformation is straightforward, it doesn't make the code very readable. The simplicity of the informal description is lost. While this code might be acceptable for machine generated and maintained FSM, it is does not scale to large finite state machines that must be maintained by humans.

With coroutines the straight forward transformation is:

typedef coro::coroutine<void(char)> coroutine_type;

enum state { A, B, C};	
void fsm(coroutine_type::self& self, char input_) {
  state m_state = A;
  while(true) {
    bool input = input_ != '0';
    switch(m_state) {
    case A:
      std::cout << (input? '0' : '0');
      m_state = input? B : A;
      break;
    case B:
      std::cout << (input? '0' : '0');
      m_state = input? C : A;
      break;
    case C:
      std::cout << (input? '0' : '1');
      m_state = input? C : A;
      break;
    }
    input_ = self.yield();
  }
}

We haven't gained much with this transformation. We have simply done moved the (implicit( external loop inside the fsm and applied a control inversion: from its internal point of view, fsm is not longer called for each input, but calls the outside for inputs (using yield())

Let's examine the code more carefully and see if we can do better. The m_state variable and its assignments are just carefully concealed goto statements:

void fsm_goto(coroutine_type::self& self, char input) {
  while(true) {
  A:
    if(input != '0') {
      std::cout << '0';
      input = self.yield();
      goto B;
    } else {
      std::cout << '0';
      input = self.yield();
      goto A;
    }
  B:
    if(input != '0') {
      std::cout << '0';
      input = self.yield();
      goto C;
    } else {
      std::cout << '0';
      input = self.yield();
      goto A;
    }
  C:
    if(input != '0') {
      std::cout << '0';
      input = self.yield();
      goto C;
    } else {
      std::cout << '1';
      input = self.yield();
      goto A;
    }
  }
}

fsm_goto has lost the state variable m_state. The current state of the FSM is stored in the instruction pointer and need not to be managed explicitly. On the other hand the control flow of the code has become explicit and arguably more readable. Then again, calling readable a code full of gotos might be a stretch. Let's complete the opera and do the final transformation:

void fsm_structured(coroutine_type::self& self, char) {
 while(true) {
   if(self.result() != '0') {
     std::cout << '0';
     self.yield();
     if(self.result() != '0') {
       std::cout << '0';
       self.yield();
       if(self.result() == '0') {
         std::cout << '1';
         self.yield();
       } else {
         std::cout << '0';
         self.yield();
       }
     } else {
       std::cout << '0';
       self.yield();
     }
   } else { 
     std::cout << '0';
     self.yield();
   }
 }
}

We used result(). The sequence of ifs represent exactly the informal requirement of matching the sequence 110.

Whether the above FSM implementation is more readable of the first implementation is arguable. But it is easier to generalize it. The repetition of if statements is a strong hint that the code should be refactored:

typedef boost::function<void(coroutine_type2::self&)> action_type;

typedef coroutine<char(char)> coroutine_type2;

void terminator(coroutine_type2::self&) {}

void match(coroutine_type2::self& self, char match, char out1, char out2 , action_type act, action_type act2) {
  if(self.result() == match) {
    self.yield(out1);
    act(self);
  } else {
    self.yield(out2);
    act2(self);
  }
}

char fsm_match(coroutine_type2::self& self, char) {
  action_type s3 (boost::bind(match, _1, '0', '1', '0', terminator, terminator));
  action_type s2 (boost::bind(match, _1, '1', '0', '0', s3, terminator));
  action_type s1 (boost::bind(match, _1, '1', '0', '0', s2, terminator));
  while(true) {
    s1(self);
  } 
}

match chooses what symbol to yield and what action to follow by checking if the last parameter to the coroutine is equal to the symbol to be matched.

The structured FSM can be extended to match more complex patterns. For example a matcher for the regular expression (01+010) can be written as:

void fsm_regexp(coroutine_type::self& self, char) {
  while(true) {
    if(self.result() == '0') {
      std::cout << '0';
      self.yield();
      if(self.result() == '1') {
        std::cout << '0';
        self.yield();
        while(self.result() == '1') {
          std::cout << '0';
          self.yield();
        }
        std::cout <<'0';
        self.yield();
        if(self.result() == '1') {
          std::cout << '0';
          self.yield();
          if(self.result() == '0') {
            std::cout << '1';
            self.yield();
          } else {
            std::cout <<'0';
            self.yield();
          } 
        } else {
          std::cout <<'0';
          self.yield();
        }
      } else {
        std::cout << '0';
        self.yield();
      }
    } else {
      std::cout <<'0';
      self.yield();
    }
  } 
}

Generalizing this example is left as an exercise for the reader.

Notice that the above FSM will fail to match the last six digits of this pattern:

011011010

This because when it sees the fourth 1, while it was expecting a 0, the state machine does not backtrack to match the 1+ pattern, but returns to the beginning of the pattern and tries to find a 0.

It is possible to implement backtracking elegantly with coroutines using a goal driven design, but it is beyond the scope of this document. See the example complex_matcher.cpp for more details.